4074. Find the median - 2
Median plays an important
role in the world of statistics. By definition, it is a value which divides an
array into two equal parts. In this problem you are to determine the current
median of some long integers.
Suppose, we have five
numbers {1, 3, 6, 2, 7}. In this case 3 is the
median as it has exactly two numbers on its each side: {1, 2} and
{6, 7}.
If there are even number of
values like {1, 3, 6, 2, 7, 8}, only one value cannot
split this array into equal two parts, so we consider the average of the middle
values {3, 6}. Thus, the median will be (3 + 6)
/ 2 = 4.5. In this problem, you have to print only the integer
part, not the fractional. As a result, according to this problem, the median
will be 4.
Input. Consists of series of
integers x (0 ≤ x < 231) and total number of integers
is no more than 106.
Output. For each input integer print
in a separate line the current value of the median. For each median value print
only its integer part.
|
Sample input |
Sample output |
|
1 3 4 60 70 50 2 |
1 2 3 3 4 27 4 |
SOLUTION
data structure – heap
Algorithm analysis
Let's simulate
the solution to the problem using a linear array. At each step, we will store
the received numbers in it in sorted form. We look for the position where the
new element needs to be inserted using a binary search. However, inserting a
new element (for example, if the array is contained in a vector data structure)
using the insert method occurs in linear time. The general solution with O(n2)
complexity will not
pass the time limit.
Let's declare
two heaps:
one will support the minimum (min-heap),
and the second will support the maximum (max-heap).
Simulate the
heaps in such way that:
·
any element of the max-heap be smaller
than any element of the min-heap
(smaller numbers are stored in the max-heap,
and large numbers in the min-heap);
·
heap sizes should
be the same. In the case of an odd number of elements, the min-heap contains one more element than
the max-heap.
When a new
element arrives, put it into the min-heap
if it is not less than the smallest element of the min-heap. Otherwise, add it to the max-heap. Then balance the heaps so that the above property of
their sizes is preserved.
·
If the size of
the max-heap is larger than the size
of the min-heap, then move the largest element of the max-heap
to the min-heap.
·
If the size of the min-heap is more than one element larger
than the size of the max-heap, then move the smallest element of the min-heap to the max-heap.
The median of the current sequence will be:
·
the smallest element of the min-heap,
if the amount of
numbers is odd;
·
the arithmetic mean of the smallest
element of the min-heap and the largest element of the max-heap, if the amount of numbers is
even.
Inserting an item into
the heap and balancing takes O(log2n)
time. The total complexity of the
algorithm will be O(n log2n).
Example
Consider the
process of computing the
median with the arrival of numbers. For convenience, when the next number
arrives, we sort the sequence. The median value is given below each sequence.
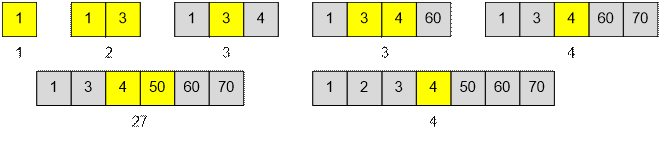
After processing
all elements of the example, the state of the heaps will be as follows:
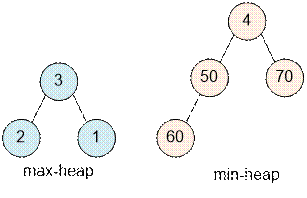
Since the number
of elements is odd, the median equals to the smallest element in the min-heap, that is, 4.
Let the next
element be 35. Since it is not less than the minimum element of the min-heap, put it into the min-heap. The size of the min-heap is 2 more than the size of the max-heap. Balancing should be done: the
smallest element of the min-heap (4)
is moved to the max-heap. That is, we remove 4 from the min-heap and add it to the max-heap.
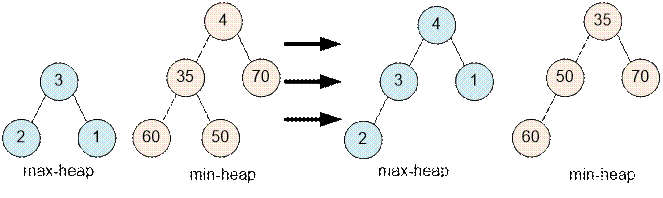
Now the total number of elements in array is even, so
the median equals to the arithmetic mean of the smallest element of the min-heap (35) and the largest element of
the max-heap (4), that is, (35 + 4) /
2 = 19 (in the problem, only the integer part of median should be printed).
Algorithm realization
Declare the min-heap mMinHeap and max-heap mMaxHeap.
priority_queue<int, vector<int>,
greater<int> > mMinHeap;
priority_queue<int, vector<int>,
less<int> > mMaxHeap;
Initialize the heaps. In the variable c count amount of numbers
received at the input. Initialize heaps with dummy
elements.
mMaxHeap.push(-MAX);
mMinHeap.push(MAX);
c
= 1;
Process the next number.
while(scanf("%d",&n) == 1)
{
Depending on the value of n, push it into one of the heaps.
if (n >=
mMinHeap.top()) mMinHeap.push(n);
else
mMaxHeap.push(n);
If the size of the max-heap is larger than the size of
the min-heap
or the size of the min-heap is more than one element larger than the size of the max-heap,
then balance them.
if(mMaxHeap.size()
> mMinHeap.size())
{
The largest element of the max-heap
is moved to the min-heap.
mMinHeap.push(mMaxHeap.top());
mMaxHeap.pop();
} else
if(mMaxHeap.size()
+ 1 < mMinHeap.size())
{
The smallest element of the min-heap
is moved to the max-heap.
mMaxHeap.push(mMinHeap.top());
mMinHeap.pop();
}
Depending on the parity of the
number of elements in the array, print the median value.
if (c % 2)
printf("%d\n",mMinHeap.top());
else printf("%d\n",(mMinHeap.top() +
mMaxHeap.top())/2);
c++;
}
Algorithm realization – multiset
This solution
works much longer than the previous one and may not pass in time. However, we’ll describe its
idea.
Store the
sequence of numbers in a multiset, the iterator iter points to the median. If set contains an even amount of numbers,
then median is the number ((*iter) +
*(iter + 1)) / 2 (recall that in the C
language with iterators only the operations -- and ++ are possible, the operation iter + 1 is impossible). To evaluate the specified expression, use second
iterator.
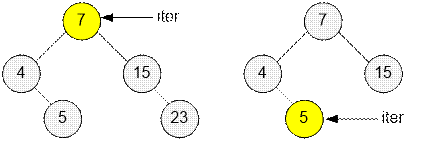
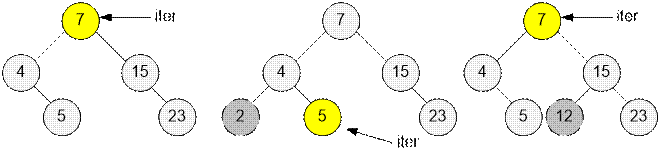
Let multiset
contains an odd
number of elements. If
insertion occurs to the left of the iterator, then the iterator should be
shifted one position to the left. If insertion occurs to the right of the
iterator, then the iterator does not change its position.
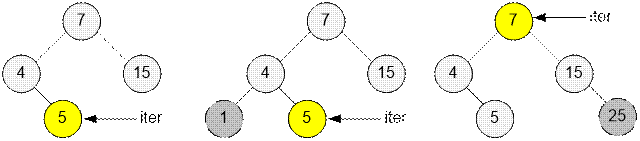
Let multiset
contains an even
number of elements. If
insertion occurs to the left of the iterator, then the iterator does not change
its position. If insertion occurs to the right of the iterator, then iterator
should be shifted one position to the right.
#include <cstdio>
#include <set>
using namespace std;
int
n, size;
multiset<int> s;
multiset<int>::iterator iter, iter1;
int
main(void)
{
scanf("%d",&n);
s.insert(n); iter = s.begin();
printf("%d\n",n);
size = 1;
while(scanf("%d",&n) == 1)
{
s.insert(n); size++;
if ((n <
*iter) && (size % 2 == 0)) iter--;
if ((n
>= *iter) && (size % 2 == 1)) iter++;
if (size
& 1) printf("%d\n",*iter);
else
{
iter1 = iter; iter1++;
printf("%d\n",(*iter
+ *iter1)/2);
}
}
return 0;
}